Autocorrelation & Independence
These are two very important and intimately related statistical concepts that I’d like to cover so folk can get a better handle on the pitfalls associated with assessment of vaccine benefit/disbenefit. Understand this and you’ll understand a great deal.
The assumption of independence of measure critically underpins all statistical analysis. This is equivalent to assuming the heights of students coming into my classroom are appearing in a random manner as they file through the door. In stats talk we say student height is an independent measure, meaning the height of one student has no bearing whatsoever on the next student coming in to class. I can thus measure heights of the first 10 of 30 students coming in to my morning class and measure the heights of the first 10 of 30 students coming in to my afternoon class and compare them. If my morning class are first year students and my afternoon class final year students then I am going to detect a difference that is meaningful and based on a real world phenomenon called growing up.
Let us now suppose I get my first year students to stand in a line of descending height such that the taller ones come through the classroom door first. I measure the first 10 to come through. For the afternoon lesson I ask my final year students to stand in a line of ascending order. I measure the first 10 to come through. In this situation I could easily end up with a sample of 10 first year students whose heights are greater than my sample of 10 final year students. The conclusion I would come to is that children shrink as they age.
Although this sounds ridiculous it is a trap that many serious studies fall into, and especially studies of vaccine benefit/disbenefit. The problem arises when I get my students to stand in order of height; that is to say I have introduced dependency in my primary measure such that the value of a student’s height is dependent on the height of the previous student.
In this simple example I have generated dependency by physically positioning the students. In the real world of infection, transmission, admission, hospitalisation, death, recovery, immunity and treatment this positioning into dependency is undertaken by the passage of time. Thus, measures varying over time cannot be assumed to be independent and this means all statistical analyses undertaken across the globe are likely invalid unless somebody decided to check. By ignoring the critical assumption of independence of measure we’re in danger of coming to the conclusion that students shrink with age in terms of vaccination. Ouch indeed!
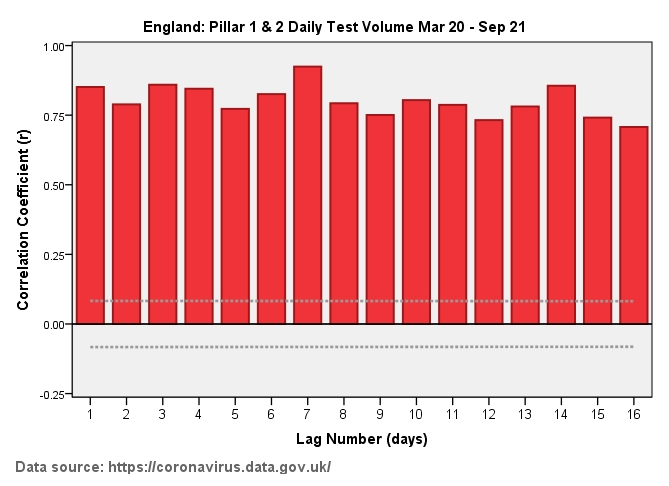
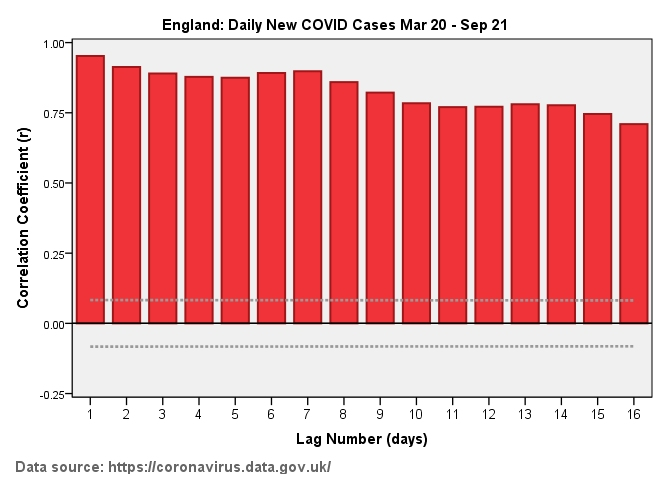
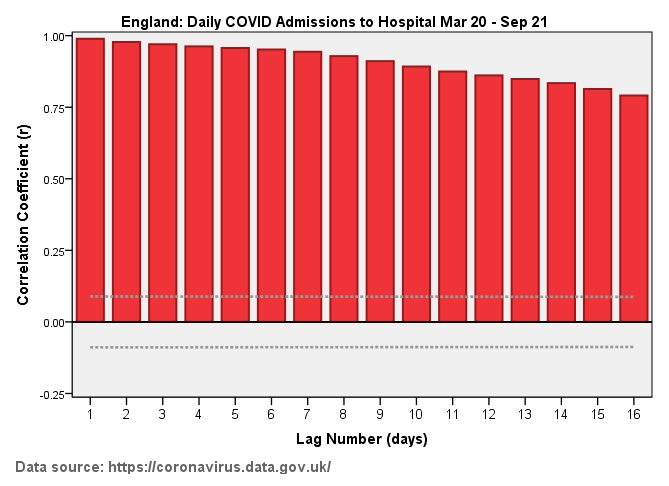
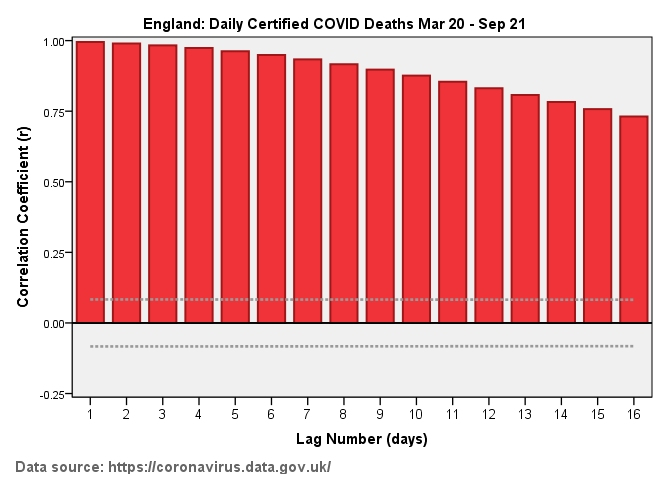
We may ask how we can determine independence of measure for a data series and this is where the concept of autocorrelation comes in. Autocorrelation simply means ‘self-correlation’; that is to say we can calculate whether the values of a series are bobbing about all over the place (independent) or whether they are exhibiting strong patterns (dependent). With this in mind I thought I’d run four popular pandemic measures through the autocorrelation procedure in my stats package, these being daily viral tests, daily COVID cases, daily COVID admissions and daily certified COVID deaths for England over the period Mar 20 – Sep 21.
You will see a palisade of positive red bars in every instance, this indicating total lack of independence of measure. Taking the first slide of the autocorrelation plot for daily viral tests we see the first red bar sticking up at a value of r = +0.85; this means the number of tests undertaken today (lag zero) is pretty much identical to the number of tests undertaken yesterday (lag 1). This palisade stretches out to lag 16 and beyond which means one week’s activity is pretty much similar to the next. We may think of this as momentum and all four examples exhibit significant momentum. This brings another level of pain, whereby we realise that data exhibiting a high degree of autocorrelation can generate phantom correlation; that is to say we may think admissions are rising because COVID cases are rising but this may not necessarily be the case!
What does this mean? Well it means that anybody not accounting for violation of the Law of Independence is going to produce reports worthy of the toilet block rather than a periodical. It means they could easily come to the conclusion that students shrink with age. I include myself in this and perhaps you can now see why I tend to use the phrase “appears to be” and judiciously use the word “seems”. Unravelling this mess is not going to be easy which is why an international panel of experts is now gathering behind the scenes. In a nutshell we haven’t got a clue as to vaccine benefit/disbenefit as yet and any organisation claiming otherwise is either as ignorant as they come or after the cash.