Exploring Excess Death (part 4)

I investigate alternative methods for estimating excess death using ONS weekly registration data from 2010 - 2023

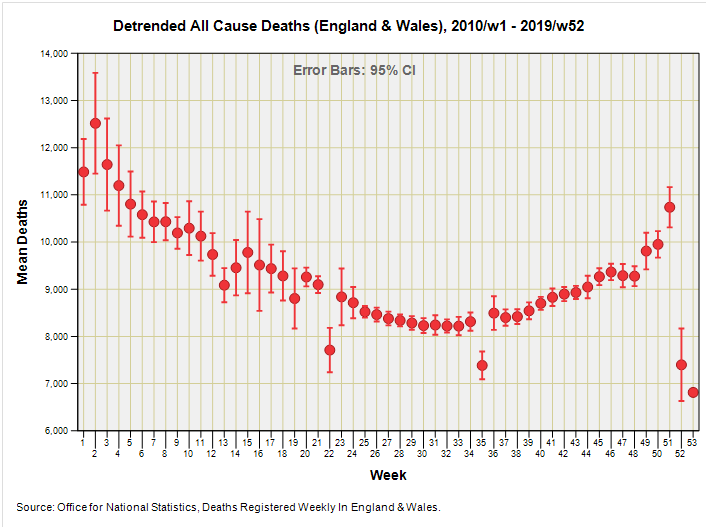
In this article I am going to derive what I shall call the seasonal mean baseline. We observed strong seasonality in the exorcised time series of part 3 as well as the colourful factored line chart also therein. Today I’m going to take the pre-pandemic period of 2010 – 2019 and scrunch the death tally down into a single mean value per week of the year, but first I need to de-trend the data that is rising at an estimated rate of between 2.28 and 2.42 deaths per week, depending on how we like to fry our statistics.

I like the taste of autoregression and the liberation from time dependency that this method brings so shall choose 2.28 deaths per week as my measure of fatal inflation (see part 3 for details). Here’s what the resulting de-trended mean weekly data looks like in the form of an error bar chart:

The lonely dot over on the far right represents 2015/w53. Note the wider error bars at the beginning and end of the year when weekly deaths can vary considerably from year to year. The cu…